はじめに
YOLOv3を実装する機会があったので、それを用いてじゃんけんの手を判別するシステムを作成してみようと思います。
YOLOv3の論文 : https://arxiv.org/abs/1804.02767
実装したリポジトリ : https://github.com/atsushi11o7/YOLOv3
実装の参考にした記事 : https://zenn.dev/opamp/articles/5198d6bf369b8e
実験
モデルは以下のように実装しました。
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.nn.modules.batchnorm import BatchNorm2d
class ResidualBlock(nn.Module):
def __init__(self, num_filters, num_blocks):
super().__init__()
self.block_list = nn.ModuleList()
for _ in range(num_blocks):
self.block_list.append(
nn.Sequential(
nn.Conv2d(num_filters, num_filters//2, 1, 1),
nn.BatchNorm2d(num_filters//2),
nn.LeakyReLU(),
nn.Conv2d(num_filters//2, num_filters, 3, 1, 1),
nn.BatchNorm2d(num_filters),
nn.LeakyReLU()
)
)
def forward(self, x):
for block in self.block_list:
x = x + block(x)
return x
class Darknet53(nn.Module):
def __init__(self):
super(Darknet53, self).__init__()
self.darknet26 = nn.Sequential(
nn.Conv2d(3, 32, 3, 1, 1),
nn.BatchNorm2d(32),
nn.LeakyReLU(),
nn.Conv2d(32, 64, 3, 2, 1),
nn.BatchNorm2d(64),
nn.LeakyReLU(),
ResidualBlock(64, 1),
nn.Conv2d(64, 128, 3, 2, 1),
nn.BatchNorm2d(128),
nn.LeakyReLU(),
ResidualBlock(128, 2),
nn.Conv2d(128, 256, 3, 2, 1),
nn.BatchNorm2d(256),
nn.LeakyReLU(),
ResidualBlock(256, 8)
)
self.darknet43 = nn.Sequential(
nn.Conv2d(256, 512, 3, 2, 1),
nn.BatchNorm2d(512),
nn.LeakyReLU(),
ResidualBlock(512, 8)
)
self.darknet52 = nn.Sequential(
nn.Conv2d(512, 1024, 3, 2, 1),
nn.BatchNorm2d(1024),
nn.LeakyReLU(),
ResidualBlock(1024, 4)
)
self.darknet_final_layer = nn.Sequential(
nn.Conv2d(1024, 1000, 1, 1, 0),
nn.BatchNorm2d(1000),
nn.LeakyReLU(),
nn.AdaptiveAvgPool2d((1, 1)),
nn.Flatten()
)
def forward(self, x):
x = self.darknet26(x)
x = self.darknet43(x)
x = self.darknet52(x)
x = self.darknet_final_layer(x)
return x# YOLOv3の実装
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.nn.modules.batchnorm import BatchNorm2d
from Darknet53 import Darknet53
class ConvBlock(nn.Module):
def __init__(self, input_block, output_block, num_blocks):
super(ConvBlock, self).__init__()
conv_block = nn.ModuleList()
for block in range(num_blocks):
in_channels = input_block if block == 0 else output_block
conv_block.append(
nn.Sequential(
nn.Conv2d(in_channels, output_block//2, 1, 1),
nn.BatchNorm2d(output_block//2),
nn.LeakyReLU(),
nn.Conv2d(output_block//2, output_block, 3, 1, 1),
nn.BatchNorm2d(output_block),
nn.LeakyReLU()
)
)
self.conv_block = nn.Sequential(*conv_block)
def forward(self, x):
return self.conv_block(x)
class YOLOv3(nn.Module):
def __init__(self, num_class = 1):
super(YOLOv3, self).__init__()
self.darknet26 = Darknet53().darknet26
self.darknet43 = Darknet53().darknet43
self.darknet52 = Darknet53().darknet52
self.conv_block = ConvBlock(1024, 1024, 3)
self.scale3_YOLO_layer = nn.Conv2d(1024, (3 * (4 + 1 + 3)), 1, 1)
self.scale2_upsampling = nn.Conv2d(1024, 256, 1, 1)
self.scale2_conv_block = ConvBlock(768, 512, 3)
self.scale2_YOLO_layer = nn.Conv2d(512, (3 * (4 + 1 + 3)), 1, 1)
self.scale1_upsampling = nn.Conv2d(512, 128, 1, 1)
self.scale1_conv_block = ConvBlock(384, 256, 3)
self.scale1_YOLO_layer = nn.Conv2d(256, (3 * (4 + 1 + 3)), 1, 1)
self.upsample = nn.Upsample(scale_factor = 2)
def forward(self, x):
x1 = self.darknet26(x)
x2 = self.darknet43(x1)
x3 = self.darknet52(x2)
x3 = self.conv_block(x3)
scale3_output = self.scale3_YOLO_layer(x3)
scale2_upsample = self.upsample(self.scale2_upsampling(x3))
x2 = torch.cat((x2, scale2_upsample), dim=1)
x2 = self.scale2_conv_block(x2)
scale2_output = self.scale2_YOLO_layer(x2)
scale1_upsample = self.upsample(self.scale1_upsampling(x2))
x1 = torch.cat((x1, scale1_upsample), dim=1)
x1 = self.scale1_conv_block(x1)
scale1_output = self.scale1_YOLO_layer(x1)
return scale3_output, scale2_output, scale1_output以下の画像はアノテーションした矩形を可視化したものです

かなり少ないですが、一つの手に対して6枚、計18枚の画像を学習に用いました。
最適化アルゴリズムはAdam、エポック数は100で試してみました。
以下は損失の経過です
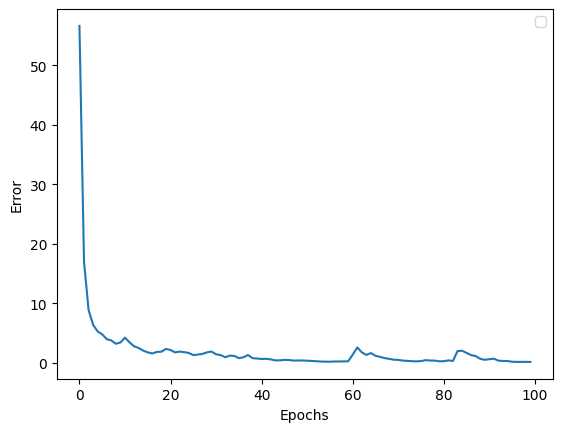
損失関数は以下のように実装しました。
def YOLOv3_loss_function(pred_list, targets_list, lambda_coord=0.1, lambda_obj=1.0, lambda_class=1.0, lambda_noobj=0.01):
coord_loss = 0
obj_loss = 0
class_loss = 0
noobj_loss = 0
B = pred_list[0].size(0)
for i in range(3):
pred = pred_list[i]
targets = targets_list[i]
for j in range(3):
pred_cut = pred[:, j*(4+1+3):(j+1)*(4+1+3), :, :] # predの分割
pred_boxes = pred_cut[:, :4, :, :] # 予測されたbboxの座標 (tx, ty, tw, th)
pred_conf_obj = pred_cut[:, 4, :, :].unsqueeze(dim=1) # 予測されたbboxの確信度
pred_classes = pred_cut[:, 5:, :, :] # クラスのスコア
targets_cut = targets[:, j*(4+1+3):(j+1)*(4+1+3), :, :] # targetsの分割
targets_boxes = targets_cut[:, :4, :, :] # targetsのbboxの座標 (tx, ty, tw, th)
targets_obj_mask = targets_cut[:, 4, :, :].unsqueeze(dim=1) # オブジェクトマスク
targets_classes = targets_cut[:, 5:, :, :] # targetsのスコア
# 位置の損失を計算
#coord_loss += lambda_coord * nn.MSELoss(reduction='sum')(targets_obj_mask * pred_boxes, targets_boxes)
coord_loss += lambda_coord * torch.sum(torch.square(pred_boxes - targets_boxes) * targets_obj_mask)
# オブジェクトの損失を計算
#obj_loss += lambda_obj * nn.BCEWithLogitsLoss(reduction='sum')(targets_obj_mask * pred_conf_obj, targets_obj_mask)
obj_loss += lambda_obj * torch.sum(-1 * torch.log(torch.sigmoid(pred_conf_obj)+ 1e-7) * targets_obj_mask)
# クラスの損失を計算
class_loss += lambda_class * torch.sum(targets_obj_mask * F.binary_cross_entropy(torch.sigmoid(pred_classes), targets_classes))
# ノンオブジェクトの損失を計算
#noobj_loss += lambda_noobj * nn.BCEWithLogitsLoss(reduction='sum')((1 - targets_obj_mask) * (1 - pred_conf_obj), 1 - targets_obj_mask)
noobj_loss += lambda_noobj * torch.sum((-1 * torch.log(1 - torch.sigmoid(pred_conf_obj)+ 1e-7)) * (1 - targets_obj_mask))
loss = coord_loss + obj_loss + class_loss + noobj_loss
return loss/B, coord_loss/B, obj_loss/B, class_loss/B, noobj_loss/B結果
以下の画像は結果の一例です。

大きい枠はチョキと判定していて、小さい枠はグーと判定しています。
パーは比較的高精度で判定できたのですが、かなり甘い結果になりました。
18枚しか学習に使用してない割にはうまくいったのでしょうか?
